Unión de conjuntos
Primer caso. Cuando los elementos de un conjunto no son los mismos que los del otro conjunto.
Ejemplo:


Simbólicamente se expresa:

Cuando los elementos de un conjunto y los de otro conjunto no son iguales o comunes, la unión de ellos forman un nuevo conjunto igual a todos los elementos de uno y otro conjunto. Este es un conjunto disjunto.
Nota. El signo que se usa para expresar la unión de dos conjuntos es una “U” modificada.
Segundo caso. Cuando alguno de los elementos del primer conjunto forman parte también del segundo conjunto.
Ejemplo:
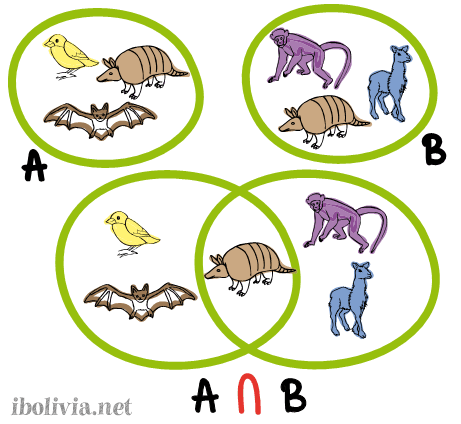
Obsérvese que tanto en el conjunto A como en el conjunto B el elemento común es el armadillo (quirquincho). Al unir estos conjuntos se representa gráficamente con un solo armadillo para los dos conjuntos. Simbólicamente representamos así:

Para la unión de 2 o más conjuntos cuando existen elementos comunes en unos y otros, se consideran sólo una vez los elementos comunes más todos los que no son comunes.
Tercer Caso. Cuando los elementos de un conjunto son también elementos de otro conjunto.
Ejemplo:
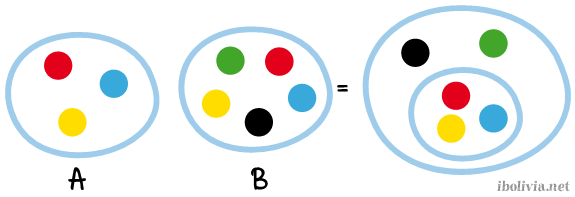

o también:

Cuando un conjunto tiene además de sus propios elementos los o todos los elementos de otro conjunto, para la unión de ellos se considera el conjunto de mayor número de elementos; puesto que el conjunto de menor número de elementos constituye un subconjunto, por tanto, incluido dentro del otro conjunto.
Cuarto caso. Cuando uno de los conjuntos es vacío.
Ejemplo:


Cuando un conjunto es vacío, equivale a que ese conjunto no tenga ningún elemento (sin valor, igual a cero). La unión con otros conjuntos da por resultado el mismo conjunto lleno.
Diagrama de Venn. Así se llama a las representaciones gráficas de las uniones de conjuntos expresada en las siguientes figuras:

Propiedades de la unión de conjuntos.
Propiedad Asociativa
Ejemplo: Sean los siguientes conjuntos:

Se puede unir primero entre sí los conjuntos A y B, y se tiene:

Luego, se une con el tercer conjunto los conjuntos ya unidos A y B, y se tiene:

Nota. También puede unirse previamente los conjuntos A y C, para luego unirse al conjunto B; nos dará siempre el mismo resultado. Simbólicamente representamos así:
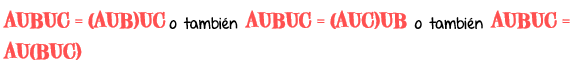
Generalización. En la unión de 3 o más conjuntos pueden unirse independientemente entre sí para luego unirse al resto de los conjuntos, sin que esto modifique el resultado final.
Propiedad conmutativa
Ejemplo:
Sean los conjuntos:


Si se cambia el orden de estos conjuntos poniendo primero el conjunto B y luego el conjunto A, tenemos:
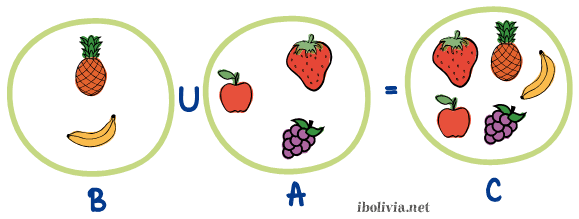
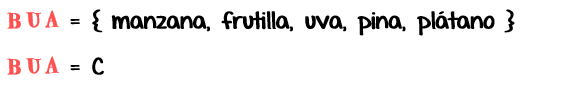
Como se observa, el conjunto C es el mismo que cuando unimos los conjuntos A y 13; por tanto, podemos expresar:

Que quiere decir: la unión del conjunto A y B es el mismo que la unión del conjunto B y A, vale decir el resultado es el mismo.
Generalización. En la unión de 2 o más conjuntos se puede alterar el orden de los conjuntos, sin que el resultado final vane.
Intersección de conjuntos
Primer caso. Los conjuntos tienen algunos elementos con características comunes a ambos. Ejemplo:

El conjunto A está formado por toda clase de máquinas de sumar, pueden ser manuales, eléctricas, electrónicas, etc.; el conjunto B tiene como elementos todas las máquinas eléctricas, pudiendo ser máquinas eléctricas de escribir, de sumar, lavadoras eléctricas, barredoras eléctricas, etc.
Si se toman en cuenta ciertas características del conjunto A con ciertas características del conjunto B, se tiene que algunas máquinas de sumar son eléctricas.
En estos 2 grupos de conjuntos ha existido una verdadera intersección de ciertos elementos con características de uno y otro conjunto.
Otros ejemplos de esta clase de intersección son:
a) Conjunto formado por: {libros de lectura en general} y conjunto: { cursos de segundo grado }; su intersección: { libros de lectura para segundo grado }
b) Conjunto de { rosas }, y conjunto de: { flores blancas } su intersección el conjunto de: { rosas de color blanca }
c) Conjunto de: { habitantes de la ciudad de Santa Cruz }, y conjunto de: { alumnos de las escuelas de Bolivia}; su intersección: { alumnos de las escuelas de Santa Cruz }
d) Conjunto de los números: { 3–4–5–9 }, y conjunto de los números: { 2–4–6–9 }; su intersección: { 4–9 }
e) Conjuntos de las letras: { a–b–c–d }, y conjunto de las letras: { a–b–d–f }, su intersección: { a–b–d }
Nota. El signo que se utiliza para designar la intersección de conjuntos es:

(como una “U” invertida) y se escribe:
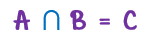
que se interpreta así: el conjunto A al intersectarse con el conjunto B da por resultado el conjunto C.
Generalización. Se llama intersección de conjuntos al conjunto formado por todos los elementos con características propias a ambos conjuntos.
Segundo caso. Un conjunto tiene todos los elementos de otro conjunto fuera de sus propios elementos. Ejemplo:

El conjunto de mamíferos forma parte del conjunto de animales, por tanto, aquél es un subconjunto.
Otros ejemplos de este caso de intersecciones son:
a) El conjunto de: { diamante–oro }, y el conjunto de: { piedras preciosas }; su intersección da el conjunto de: { piedras preciosas }, por cuanto el diamante y el oro forman parte de las piedras preciosas.
b) El conjunto: { piernas }, el conjunto: {brazos } y el conjunto: { cuerpo humano } da por intersección el conjunto: { cuerpo humano }, puesto que los otros conjuntos son subconjuntos del conjunto cuerpo humano.
c) Sea:
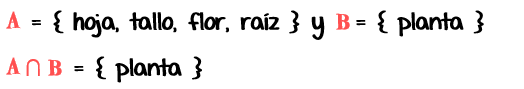
d) Sea:

al intersectar tenemos

Generalización. Cuando se intersectan 2 o más conjuntos cuyos elementos forman parte de otro conjunto, el resultado es el conjunto que tiene el mayor número de elementos.
Tercer caso. Los conjuntos no poseen elementos comunes. Ejemplo:

Otros ejemplos de este caso son:
a) Sea:

b) Sea:

Generalización. Cuando 2 o más conjuntos tienen elementos que no sean comunes entre los conjuntos, el resultado es un conjunto vacío.
Diagrama de Venn
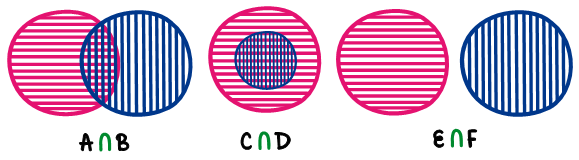
Propiedades de la intersección de conjuntos
Propiedad Asociativa
Ejemplo:
Sean los conjuntos:
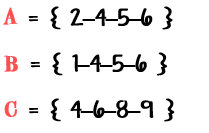
Intersectemos primeramente A y B
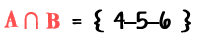
Luego este resultado intersectemos con el conjunto C

Gráficamente representamos así:

Primero: intersectar los conjuntos A y B:

Segundo: intersectar con el conjunto C

Generalización. Por la propiedad asociativa las intersecciones de 3 o más conjuntos se pueden realizar intersectando independientemente entre sí, para luego intersectar con el resto de los conjuntos sin que el resultado final varíe.
Propiedad conmutativa.
Ejemplo: sea los conjuntos:

Su intersección entre A y B es:
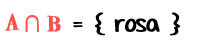
Al alterar el orden de los conjuntos se tiene:
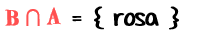
Gráficamente representamos así:

Generalización. La propiedad conmutativa de la intersección dice: si se altera el orden de 2 o más conjuntos, el resultado de su intersección no varía.