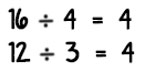Se tiene un conjunto de aulas señaladas por medio de las letras:

Y otro conjunto de cursos:
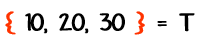
Tomando cada una de las aulas del conjunto Z con cada uno de los cursos del conjunto T se forma:
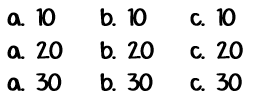
Se ha formado, pues, un nuevo conjunto asociando, en un orden estricto, un elemento del conjunto Z con un elemento del conjunto T.
El conjunto R así formado se llama producto cartesiano de los conjuntos Z y T.
Se observa que cada elemento del conjunto R está compuesto de un elemento de Z y un elemento de T.
Los elementos de un producto cartesiano son siempre pares.
El conjunto producto se presenta de esta manera:
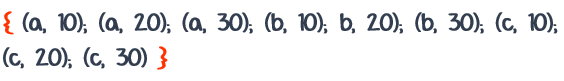
Se lee: R es el producto cartesiano de Z por T.
El producto cartesiano no tiene las propiedades conmutativa y asociativa.
La asociación de cada elemento del conjunto Z con cada elemento del conjunto T se puede representar también con flechas, en esta forma:
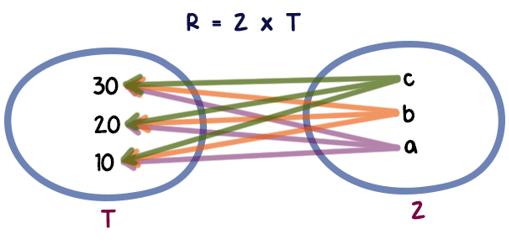
El sentido de la flecha indica el orden en que es necesario tomar los elementos para formar los pares.
Se puede hacer la representación de todos los pares y de una manera ordenada y sistemática, mediante el siguiente cuadro:

A manera do simplificar, en vez de escribir cada par, se puede también sustituirlo por un punto.

Interpretación de una gráfica
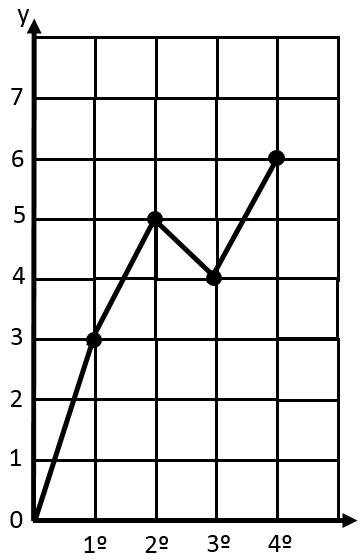
El alumno José Vázquez obtuvo el primer bimestre la nota de 3, el segundo 5, el tercer bimestre 4 y el cuarto 6.
Para una interpretación más objetiva se representa de la siguiente manera:
Conjunto: Colección, grupo, reunión de objetos; pueden ser también nombres, números, símbolos, etc.
Elemento: Unidad, o unidades que forman un conjunto.
Conjunto unitario: Posee sólo un elemento.
Subconjunto: Conjunto que forma parte de otro conjunto.
Intersección de conjuntos: Intersección de dos conjuntos A y B, cuyos elementos pertenecen a la vez a A y B.
Asociativa: Agrupa 2 términos consecutivos cualquiera, sin cambiar el resultado.
Conmutativa: Permite alterar el orden de los términos, pero sin cambiar el resultado.
Vocabulario y Simbología