Intuición del concepto de “mitad” y “cuarto”
Primera representación gráfica:

Explicación:
a) Un queso se ha dividido o partido en dos partes iguales;
b) Cada una de las partes representa la “mitad” del queso;
c) Uniendo las dos mitades del queso se tiene nuevamente el queso entero;
d) Para su representación numérica, la unidad (1) significa el entero que se coloca encima de la rayita llamada raya de quebrado. El número 2 colocado debajo de esta rayita, significa que el entero está dividido en dos partes iguales.
Conclusión. Dividiendo un entero en dos partes iguales, cada una de las partes se llama mitad, y se representa numéricamente:

Segunda representación gráfica.

Explicación:
a) La mitad del queso 1/2 se vuelve a dividir en otras dos partes iguales;
b) Dividiendo las dos mitades en otras dos cada una de ellas, se tiene que el entero o el queso ha sido dividido en 4 partes;
c) Designar a cada una de esas partes “cuarto” o “cuarta parte”;
d) Para su representación numérica la unidad (1) significa que es el entero, escrito encima de la raya de quebrado. El número 4 colocado debajo de la raya de quebrado, significa que el entero está dividido en cuatro partes iguales.
Conclusión: Dividiendo un entero en cuatro partes iguales, cada una de las partes se llama cuarto, y se representa numéricamente:
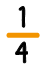
Nota: Conforme se vaya graduando la enseñanza de las fracciones tendrá que objetivizarse en la misma forma para las fracciones:

Concepto “mitad” (1/2) para la aplicación en conjuntos.
Ejemplo:
El conjunto de 8 libros repartirlo o dividirlo entre dos alumnos:
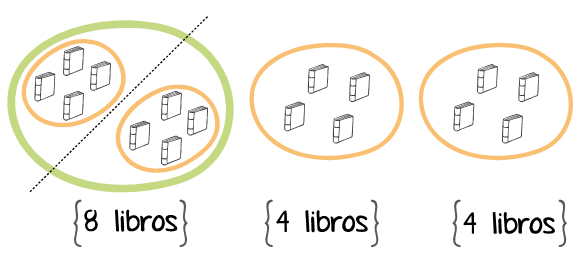
Explicación:
a) El conjunto de libros está formado por 8 elementos;
b) Formando dos subconjuntos de igual número de libros, significa dividir el conjunto en dos partes iguales;
c) Cada parte o 1/2 del conjunto representa un subconjunto, con 4 elementos cada uno;
d) La mitad del conjunto de 8 elementos es, por tanto, un subconjunto con 4 elementos.
Conclusión: Encontrar o sacar la mitad de un conjunto significa dividir en dos partes iguales el conjunto; los elementos que quedan en cualesquiera de las partes divididas constituye la mitad o un medio (1/2) del conjunto.
Nota. En igual forma intuir el 1/3, 1/4, 1/5, etc., de un conjunto, cuidando que sea divisible el conjunto.