Problema Nº 1. Un avión del L.A.B. transportó 28 pasajeros en la ruta Sucre – Cochabamba; por pasajes solamente habíase recaudado, en ese vuelo, la suma de Bs. 6.938,40. ¿Cuánto habrá pagado cada pasajero?
Solución:
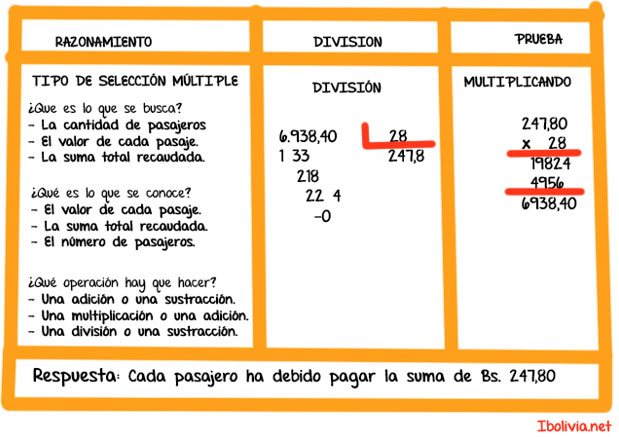
Observaciones
a) Cuando se presenta esta división de un número decimal entre un entero, se procede exactamente como en la división de enteros, teniendo el cuidado de poner la coma en el cociente, al tiempo de bajar el primer decimal del dividendo.
b) El nuevo tipo de razonamiento del sistema de la “selección múltiple” es recomendable por el Instituto de Investigaciones Pedagógicas. Como ejemplar modelo, para el maestro de Primaria, utilizamos en el texto únicamente dos casos primiciales.
c) En el razonamiento, el alumno debe habituarse a discriminar las relaciones que existen entre los datos, para formar conciencia de la operación a efectuarse. “Ello se consigue, con resultados favorables –dice el Prof. César Chávez–, por medio de otro tipo de razonamiento: el de la selección múltiple, cuya bondad y validez ha sido demostrada y reconocida por la pedagogía experimental y que, sin embargo, aún no está generalizado en nuestra práctica docente”.
Problema N º 2. Un almacén, por concepto de venta de 31,6 litros de aceite, recibió la suma de 158 Bs. ¿A cuánto habrá vendido cada litro de aceite?
Solución:

Observaciones
a) El divisor, en el problema anterior, era decimal y el dividendo entero.
b) No se pudo hacer de hecho la división, por tener el divisor un decimal.
c) Se aumentó un cero al dividendo y se suprimió la coma decimal en el divisor pudiendo efectuarse recién la división.
Generalización. Cuando se presenta el caso de dividir un entero entre un decimal, se deben hacer desaparecer los decimales del divisor suprimiendo la coma decimal y aumentando al dividendo tantos ceros como números decimales se hayan suprimido en el divisor.
Problema N º 3. Cierto joven compró un casimir nacional, para mandar a confeccionar un terno con dos pantalones: pagó por los 4,35 m. que adquirió la suma de 592,75. ¿A cómo le habrán dado cada metro?

Observaciones
a) Ambos términos de la división contienen decimales.
b) No se pudo hacer directamente la división por tener el divisor decimales.
c) Para poder efectuar la operación se han contado los decimales del divisor, que son dos, para recorrer la coma decimal del dividendo también dos lugares hacia la derecha. Al hacer esta operación, se ha convertido el divisor en número entero.
Generalización. Cuando se presenta este caso de división, lo primero que se debe hacer es contar los decimales que contenga el divisor, para luego recorrer de izquierda a derecha la coma decimal del dividendo tantos lugares como decimales se hayan suprimido. En seguida se efectuará la división corriente. No importa si al recorrer la coma decimal del dividendo, éste quede como decimal.
Pruebas
a) Por la exclusión de nueves.
b) Multiplicando el cociente por el divisor y sumando el residuo (si existe).
c) Mediante otra división: el dividendo entre el cociente dará el divisor (esta prueba es cabal sólo en el caso de que el residuo sea menor que el cociente; en otros casos es inexacta).
Nota
1º En la división de decimales entre sí, no importa que el dividendo quede con uno o más decimales una vez recorrida la coma decimal. En ese caso se hará la división como se indica en el problema Nº 1.
2º El hecho de suprimir la coma decimal en el divisor y aumentar ceros en el dividendo, se basa en el principio aritmético que dice: “si se multiplican ambos términos de una división, por un mismo número, el resultado no varía”. En estos casos se multiplican por 10, 100, 1.000, etc.
3º En caso de que el dividendo no tenga decimales y se quiera obtener el resultado con fracción decimal, se tendrá que agregar ceros a la última cifra bajada del dividendo, poniendo inmediatamente la coma decimal en el cociente.
Ejercicios
(Según progresiva seriación del grado de dificultad.)
1er Caso:
— Dividiendo con 2 cifras decimales:

— Dividiendo exclusivamente decimal, con 1 cifra:

— Dividiendo decimal, con 2 cifras, siendo la primera cero:

2do Caso:
— Divisor entero, con 1 cifra decimal:

— Divisor exclusivamente decimal, con 2 cifras:
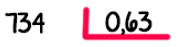
— Divisor con 2 decimales, siendo el primer decimal cero:

— Divisor decimal de 3 cifras:

3er Caso:
— Dividendo y divisor con igual número de decimales:
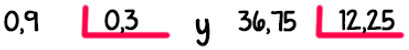
— Dividendo y divisor con número desigual de decimales.

Nota:
a) Esta serie de dificultad progresiva será también aplicable, por similitud, a la multiplicación.
b) En estas muestras de ejercicios encontrará el institutor sugestiones concretas que le orienten su cotidiana labor didáctica en el uso de los mecanismos aritméticos.
c) En EE.UU. emplean el punto, en vez de coma, para separar cifras decimales.