(máximo común divisor aplicando conceptos de conjuntos)
1) Sean los números 12 y 40; buscar el mayor número que pueda dividir a ambos, debiendo ser éste común para los dos números.

2) Si aplicamos la intersección de conjuntos para los divisores de los números 12 y 60, tendremos:

Gráficamente se representa así:
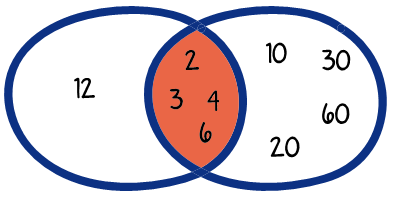
Los divisores comunes son: 2–3–4 y 6; siendo el “máximo” el número 6.
3) La operación de conjuntos que lleva a determinar el M. C. D. es la intersección, porque en él aparecen elementos comunes, considerando los divisores de cada número.
4) Tomando el mayor o “máximo” número intersectado, se llega a determinar que ese número es el Máximo Común Divisor.
Definición. Se llama M.C.D. (máximo común divisor) de 2 o más números al mayor divisor común de esos números dados.