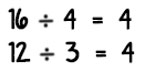Adición
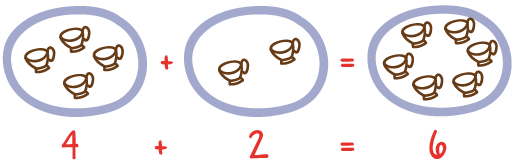
Observación:
1) Se utiliza el signo + (más) que significa reunir, agrupar, juntar.
2) Los conjuntos deben tener la misma clase de elementos, es decir deben ser homogéneos.
3) Los elementos de un conjunto se agrupan con los del otro conjunto, para formar un tercer conjunto que es su resultado.
Propiedades de la adición. Al igual que en la unión e intersección de conjuntos, la suma goza de las dos propiedades fundamentales: asociativa y conmutativa.
Sustracción
Aplicación de la relación de correspondencia en la sustracción. Presentar en un segundo conjunto los elementos que se deseen quitar del primer conjunto:

Observación:
1) Los elementos cuadrado y círculo del primer conjunto tienen una relación de correspondencia con el cuadrado y círculo del segundo conjunto.
2) Los elementos estrella, triángulo y luna no tienen ninguna relación de correspondencia con los elementos del segundo conjunto.
3) Los tres elementos del primer conjunto que no tienen relación de correspondencia, se los representa en un tercer conjunto que viene a ser el resultado de la sustracción.
Se representa simbólicamente así:

menos:

igual a

Generalizando con la aplicación de letras tenemos:

Igual:

Observación.
1) En la operación de sustracción se utiliza el signo – (menos) que significa quitar, sustraer, restar.
2) En los conjuntos disjuntos las operaciones de resta tienen que intuirse o enseñarse quitando los elementos que tienen su relación de correspondencia con el otro conjunto, para concluir que el resultado de esa operación es otro conjunto disjunto que no tiene relación de correspondencia.
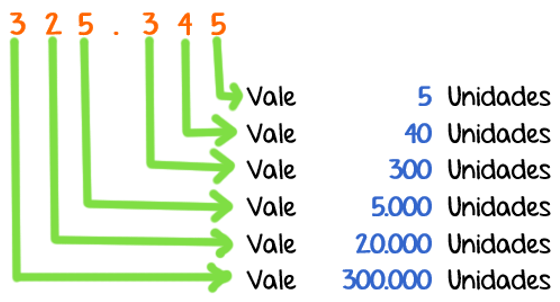
3) Al tener un conjunto los mismos elementos, es decir que éstos sean homogéneos, se puede representar numéricamente, asignándole a cada elemento el valor de una unidad.
Ejemplo: en un conjunto existen 8 monedas, y en el otro 3 monedas, los mismos se representan numéricamente:
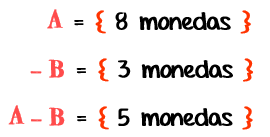
También se puede intuir gráficamente aplicando el mismo concepto de la relación de correspondencia, en la que cada elemento de conjunto es representado por una moneda. Al establecer la relación de correspondencia con el otro conjunto, el resultado será el número de monedas que no tienen correspondencia.
Comprobación de las operaciones de adición y sustracción. Adición y sustracción son operaciones que tienen un proceso inverso, característica que sirve para comprobar la exactitud de estas operaciones.
Prueba de la adición
Sea la adición de los conjuntos A y B
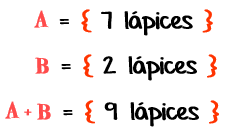
Se comprueba restando el resultado de 9 lápices nuevos cualquiera de los otros conjuntos, el nuevo resultado será igual al otro conjunto.
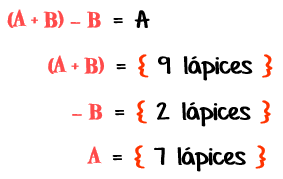
Prueba de la sustracción
Sea la sustracción de los conjuntos A y B

Se compraba sumando el resultado de 11 alumnos con el conjunto que tiene menos número de elementos, el resultado será igual al otro conjunto:

Multiplicación
Ejemplo, sea los conjuntos:


Sumar:
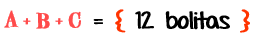
Observación:
a) Vemos que los 3 conjuntos son iguales, es decir que tienen 4 elementos cada uno;
b) Por tanto el conjunto A es igual al conjunto B y C;
c) En consecuencia si se repite 3 veces la suma de un sólo conjunto, puesto que son iguales los otros conjuntos, obtenemos el resultado de 12 bolitas, es decir:

d) Remplazar la palabra "veces" con el signo de la multiplicación “x”, colocado entre los 2 números y que se leerá “por”; se tiene:
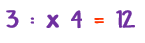
(tres “por” cuatro igual a doce)
Conclusión. La multiplicación no es más que una suma abreviada.
División
Sean los siguientes conjuntos:
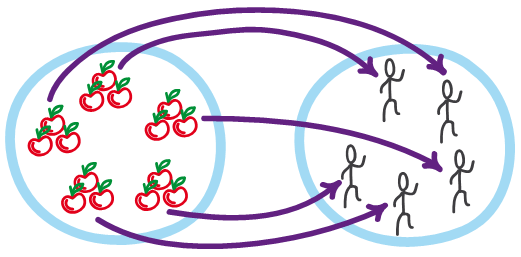

Se quiere repartir las 15 manzanas entre los 5 alumnos.
Observación:
a) La correspondencia del primer conjunto A con el conjunto B es de 3 manzanas para cada alumno.
b) Si se considera en subconjuntos el conjunto de manzanas de tal manera que exista la misma relación de correspondencia de 3 a 1, se obtiene los 5 subconjuntos con igual número de elementos:
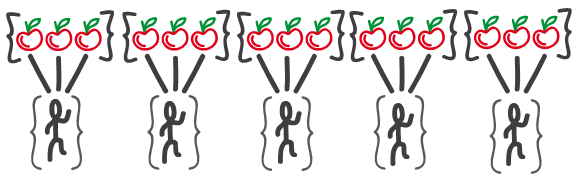
c) En la distribución de las 15 manzanas entre los 5 alumnos, se han formado 5 subconjuntos de a 3 manzanas cada uno, lo que quiere decir que a los 5 alumnos les tocará a 3 manzanas.
d) Simbólicamente esta distribución expresamos:

que pueden escribirse bajo las siguientes formas, cuyos signos significan “división”.

Conclusión. Dividir significa repartir, distribuir o separar en partes iguales. Por consiguiente, la división no es más que una repartición del conjunto en varios subconjuntos cuyo número de elementos sean iguales. El número de elementos que corresponde a cada sub-conjunto se torna en resultado de la operación.
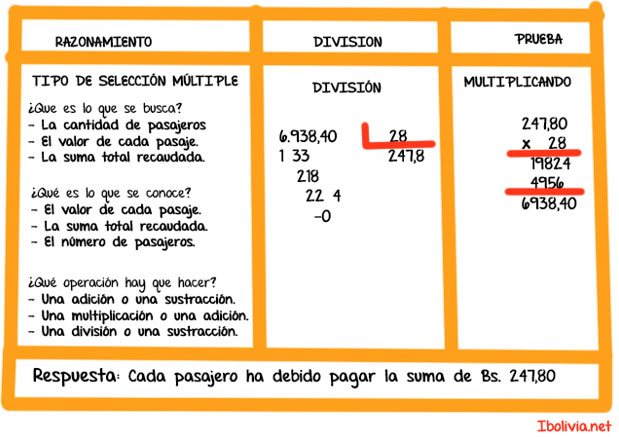
Prueba en la multiplicación y división. Como la multiplicación y la división tienen un proceso inverso, se aprovecha esta característica para la comprobación de la exactitud de las operaciones, y así tenemos:
Prueba de la multiplicación.

Si dividimos el resultado del conjunto { 72 } entre uno de los conjuntos de la operación, tendremos:
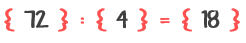
o también:

Se observa que el resultado es igual al otro conjunto, hecho que nos permite decir que la multiplicación está correcta.
Prueba de la división

Si multiplicamos el conjunto { 7 } por el conjunto { 3 } que es el menor de la operación de división, tendremos:

Se observa que el resultado es igual al otro conjunto, hecho que nos permite decir que la división está correcta.