Concepto sobre conjuntos.
Ejemplo:
Este es un equipo de fútbol boliviano, cuyos integrantes son todos bolivianos. Este Conjunto ganó a los campeones mundiales de Argentina y Brasil en el Estadio Olímpico de La Paz, por las eliminatorias de la Copa América del año 1979.
Este Conjunto fue dirigido por el técnico Ramiro Blacutt y estuvo compuesto por los jugadores: Carlos Conrado Jiménez, Evert Hoyos, Remberto Arispe, Ramiro Vargas, Edwin Espinoza, Edgar Vaca, Windsor Del Llano, Edwin Romero, Luis Gonzales, Carlos Aragonés, Carlos Borja, Jesús Reynaldo, Miguel Aguilar, Pablo Baldivieso, Silvio Rojas, Eduardo Angulo, Ovidio Mezza, Andrés Gallardo, David Paniagua y Rogelio Delfin.
Otros ejemplos: Un ramo de rosas forma un Conjunto floral, el conjunto de músicos que actúan en una fiesta para amenizarla forman una orquesta; el Conjunto formado por los hijos, el padre y la madre forman la familia; también forman un conjunto tres sillas, o cinco pupitres; así como el conjunto de todos los cursos forman una escuela.
Las vocales A, E, I, O, U forman parte de un Conjunto, así como todas las letras de nuestro alfabeto.
El conjunto pude estar formado por uno, dos o más Elementos. En el conjunto formado por las 5 vocales de nuestro alfabeto, cada una de ellas constituye un Elemento, y las 5 vocales serán los 5 elementos de los que está formado el Conjunto.
Generalidades. Con los ejemplos que acabamos de dar se desprenden las siguientes generalizaciones:
Conjunto: es la reunión o agrupación de personas, animales o cosas, concretas o abstractas, que se unen con o sin características comunes.
Elemento: es la parte que integra un conjunto. La reunión de los elementos forman un solo todo que se llama Conjunto.
Sugerencia didáctica. “Existe un conjunto intermedio entre el mundo de los objetos y el de los números: es el mundo de los Conjuntos”. (Dienes)
Para llegar al número hay que pasar por la realidad de la cual es una cualidad.
El ejercicio intenso de Conjuntos facilita el paso del mundo físico al mundo matemático.
Abstracción de conceptos. Aprendamos a abstraer los conceptos, es decir, aprender a razonar en forma general. Para esto nos valdremos del siguiente gráfico:

Los 6 lápices de colores forman un Conjunto que para su representación gráfica dentro del concepto de conjuntos se los encierra en óvalos o círculos.
Al decir que el conjunto está formado por 6 lápices de color, nos expresamos en forma concreta. Pero si designamos a ese conjunto simplemente con una letra, por ejemplo, la letra A, hablaremos de un Conjunto A, en forma abstracta, que puede ser una representación interpretativa de algo concreto.
Para designar un conjunto se utiliza siempre y por convención las letras mayúsculas de nuestro alfabeto.
Los elementos de los que está formado un conjunto se los interpreta con símbolos o letras en minúsculas.
Al designar a los lápices de color una letra de nuestro alfabeto, les damos un concepto abstracto, así, por ejemplo: la letra a, para el lápiz de color rojo; b para el azul; c para el café; d para el verde; e para el amarillo; y, finalmente el anaranjado estará representado por la letra f. Al conjunto de todos los elementos hemos designado con la letra A, cuya representación gráfica es la siguiente:
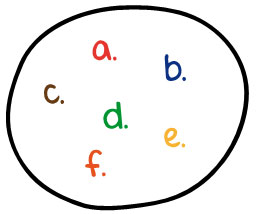
Representación gráfica en forma simbólica del Conjunto de los seis lápices.
Se puede representar simbólicamente en la siguiente forma:

Que se lee así: el conjunto A tiene o está formado por los elementos a, b, c, d, e, f. Los elementos de un conjunto siempre van dentro de llaves.
Como previamente se ha designado a los lápices de color con estas letras, sabemos que cada letra representa a un lápiz de color. Pero, si no tuviéramos el antecedente anterior concreto, y si nos presentaran el conjunto simplemente en forma simbólica, podríamos atribuir perfectamente a cada letra un elemento completamente distinto al de los lápices. Es de esta manera que generalizamos o abstraemos los conceptos.
Otro ejemplo: Designemos a la escuela donde estudiamos, con la letra X, formada por el primer curso y su paralelo; por el segundo curso y su paralelo; por el tercer curso y su paralelo; y por el cuarto, quinto y sexto cursos. Para representar simbólicamente utilicemos los números ordinarios para cada curso principal y la letra “B” para los cursos paralelos, y tendremos:

Y se lee: el conjunto X está formado por los elementos 1er., 1er. “B”, 2do., 2do. “B” ... etc. (razonamiento abstracto). Como sabemos que la X representa a la escuela, diremos en un razonamiento concreto que el CONJUNTO de la Escuela está formado por el primer curso, y su paralelo “B”; por el segundo curso y su paralelo “B”; etc., etc.
Subconjunto
Ejemplo:
Representemos los cursos de una escuela con estos gráficos siguientes:

En sí cada curso forma un CONJUNTO; sus elementos pueden ser los alumnos, los pupitres, los cuadros, etc. Consideremos ahora que estos cursos son parte de una escuela, es decir que se convierten en elementos de un conjunto más grande que es la escuela; cada curso considerado dentro el CONJUNTO de la Escuela, se convierte en un SUBCONJUNTO. Gráficamente tendremos:

Conjunto Escuela
Concepto de Subconjunto. Por tanto, podemos definir al Sub-conjunto como un conjunto menor considerado dentro de otro conjunto mayor.
Relación e inclusión
Ejemplo:
A = {Alumnos de toda la Escuela}
B = {Alumnos del quinto curso de esa misma escuela}
Gráficamente representamos:

Como se observa, el conjunto B está incluido en el conjunto A; es decir, el conjunto formado por los alumnos del quinto curso están incluidos dentro del conjunto de los alumnos de la escuela. Para expresar esta relación de inclusión se utiliza el signo c, escribiéndose así:

que se lee: el conjunto B está incluido en el conjunto A; por tanto, B es un SUBCONJUNTO.
Otro ejemplo:
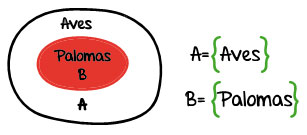
La relación de inclusión se establece entre conjuntos, constituyendo un subconjunto aquél que está incluido dentro de otro conjunto.
Relación de pertenencia. Así como la relación de inclusión se establece entre dos o más conjuntos, también se establece la relación entre los elementos y el conjunto del que forman parte, en este caso se refiere a una relación de pertenencia.
En el ejemplo del conjunto de los 6 lápices de colores podemos decir que el elemento a pertenece al conjunto A; esto quiere decir: el lápiz de color rojo pertenece al conjunto de los 6 lápices de color.
El signo que se utiliza para simbolizar la pertenencia de un elemento a un conjunto es:
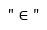
que quiere decir: “pertenece al conjunto”; la expresión anterior se escribe:

De igual manera para decir que el lápiz de color azul (b), pertenece al conjunto A, se escribe:

Para designar que un elemento no pertenece a un conjunto se utiliza el mismo signo, pero con una pequeña raya oblicua atravesada:
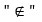
que quiere decir: “no pertenece al conjunto”. Así decimos:

Clases de Conjuntos según el número de elementos
Ejemplos:

Concepto sobre Conjunto finito. Es el conjunto que está formado por un número determinado de elementos. Ejemplos: las vocales; los días de la semana, un número determinado de objetos, etc.
Concepto sobre conjunto infinito. Es el conjunto formado por un número de elementos a los cuales siempre se puede añadir un elemento más sin que éste constituya el último elemento. Ejemplo: la sucesión de los números naturales.
Conceptos sobre conjunto vacío. Es el conjunto que carece de elementos. Equivale a CERO elementos. Se expresa con el signo:

Concepto sobre conjunto unitario. Es el conjunto formado por un solo elemento. Ejemplo: una persona; una máquina; un curso, etc.
Concepto sobre conjunto universal. Es el conjunto representado por elementos de la misma especie. Ejemplos: reloj marca Omega, reloj marca Clima, reloj marca Oris; perro Danés, perro Bull-dog, perro Galgo, perro Perdiguero, etc. El conjunto universal se representa generalmente en un rectángulo.
Determinación por extensión

Se lee: R es el conjunto al que pertenecen los elementos: a, u, e, i, o.
Cuando se tienen conjuntos con pocos elementos y se representan por medio de llaves ({ }) se dice que estos conjuntos están determinados por extensión.
Determinación por comprensión

En este caso todos los elementos son letras del abecedario con un conjunto que tiene un solo elemento: la palabra vocal:
Los matemáticos escriben en esta forma:

Se lee: T es el conjunto de elementos “equis” tales que las “equis” son letras vocales del abecedario castellano.
A esta forma de determinar un conjunto se denomina determinación por comprensión.
Correspondencia de elementos entre conjuntos.
Primer Caso.
Ejemplo:

Explicación del gráfico. El 4to. curso de la escuela tiene un profesor, así como el 5to. curso tiene su propio profesor y el 6to. curso igualmente. Al toque de la campana para la entrada a clase estos 3 profesores se dirigen cada uno a sus respectivos cursos, sin que el profesor del 5to. curso por ejemplo se vaya al 4to. o sexto curso. Existe una correspondencia del conjunto de profesores con el conjunto de las aulas, de tal manera que a cada curso corresponde un profesor.
A esta correspondencia de conjunto se llama: “coordinación de conjuntos”; en el ejemplo anterior existe coordinación de conjuntos con igual número de elementos. Existe una relación o correspondencia de IGUALDAD. El signo de igualdad es: = (se lee Igual).
Segundo Caso
Ejemplo:

Explicación del gráfico. El conjunto formado por el 4to., 5to. y 6to. cursos, tiene una relación común con un solo elemento: el profesor de música, que forma el otro conjunto. El profesor de música es al mismo tiempo profesor del 4to., 5to., y 6to. cursos.
A esta correspondencia de conjuntos se denomina “conjuntos coordinables” o “coordinación de conjuntos”, en los cuales existe una relación de 3 a 1. Existe una relación de más cursos del primer conjunto, con un solo profesor del segundo conjunto; la correspondencia es de “más que...” o “mayor que...”. Su signo es: >.
Tercer Caso.
Ejemplo:
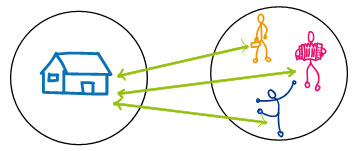
Explicación del gráfico. El 6to. curso tiene: su profesor de curso, un profesor de música y un profesor de educación física. La relación del 6to. curso es estable con 3 profesores.
A esta correspondencia de conjuntos se denomina: “coordinación de conjuntos” o “conjuntos coordinables” en una relación de 1 a 3. Existe una relación de menos cursos del primer conjunto, con más profesores del segundo conjunto. La correspondencia es de “menos que” o “menor que”. Su signo es: <.
Toda relación de correspondencia entre 2 o más conjuntos sea de igualdad, o que el primer conjunto esté relacionado con elementos “mayores que” o “menores que” los elementos de otros conjuntos, supone necesariamente que exista una afinidad o algo común entre los elementos de dichos conjuntos.
Ejemplos de correspondencia de elementos entre conjuntos
a) Alumnos de cada curso con su escuela a la que pertenecen;
b) Las personas y sus respectivas edades;
c) El peso de las personas con las edades;
d) Las ciudades o capitales de departamentos con su respectivo departamento;
e) Un candado o una chapa tiene por relación o correspondencia directa únicamente su llave o sus llaves duplicadas;
f) Un calzado tiene forzosamente su correspondencia con el otro calzado para formar un par del mismo número y modelo.
Recomendación para el maestro. Trate en este tema de afianzar la correspondencia lógica de un conjunto con otro u otros, atribuyendo luego distintos elementos de otros conjuntos para demostrar la “no correspondencia” entre los elementos de esos conjuntos. Denominar a estos conjuntos: “conjuntos no coordinables”. (Ej.: no existe relación de correspondencia entre la ciudad de La Paz como un elemento de conjunto de ciudades de Bolivia con el conjunto de la República del Brasil. Brasil y La Paz son conjuntos no coordinables).