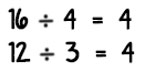Operaciones numéricas fundamentales.
Ejemplos:
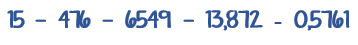
Las cifras o guarismos son signos convencionales empleados para representar a los números, destinados a indicar valores o cantidades y con los cuales se efectúan las operaciones fundamentales de la aritmética.
Son diez los signos básicos de la numeración, llamándose a estos números dígitos; ellos son:

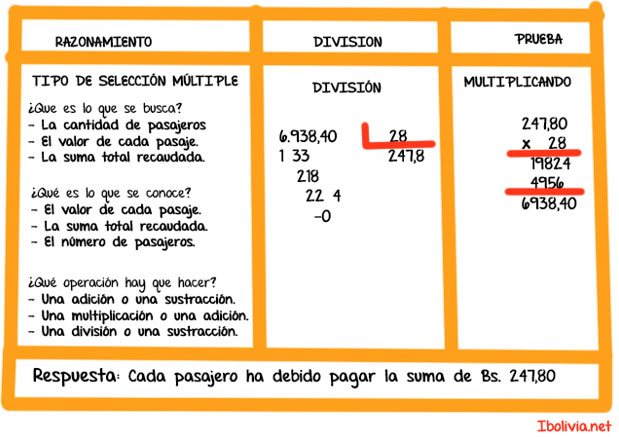
Lectura y escritura de cantidades. Es necesario tener presente la colocación relativa que toma cada cifra en una cantidad; para ello nos ayudará la siguiente tabla:
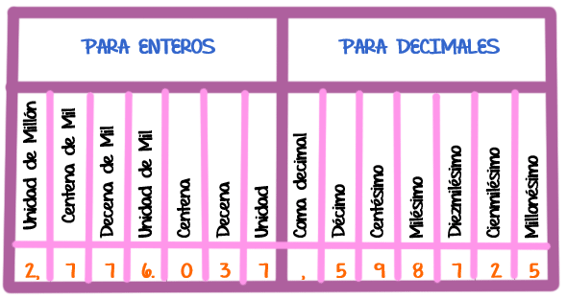
Esta cantidad se lee: 2 millones, 776 mil, 37 enteros; 598 mil, 725 millonésimos.
Para la lectura de una cantidad cualquiera, se deben observar las siguientes indicaciones de carácter general, las mismas que sirven para la escritura:
1. La coma decimal (,) es la que separa las cantidades enteras de las decimales, escribiéndose éstas a la derecha y aquéllas a la izquierda de la coma decimal (,).
2. En los números enteros, a partir de las unidades se hará la separación de tres en tres cifras, colocando al primer grupo el punto (.) de mil; al segundo el “1” de millón; al tercer grupo el . de mil de millón; al cuarto el “2” de billón. (El “1” y el “2” serán números pequeños que se colocarán ya en la parte superior o ya en la inferior.)
3. Teniendo ordenado el número o cantidad a leerse, se designará a cada grupo luego de leer sus tres cifras con las palabras: “billón”; “mil millones”, “millones”, “mil”, respectivamente.
4. La lectura de la parte decimal se efectuará en igual forma que la de los enteros, agregando luego la palabra de la columna que ocupa la última cifra decimal.
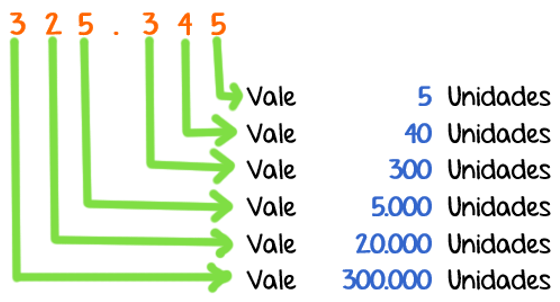
Valor absoluto y relativo de los números. Si analizamos la cantidad:

se observa que cada uno de sus números por separado guarda su valor independientemente de los demás; así el N.° 2, vale 2; el N.° 4, vale como 4; el 7 como 7, etc. Esta conservación de valores de los números, sin tomar en cuenta la posición que ocupan en una cantidad, se estima como “valor absoluto” de los números.
En cambio, si consideramos el N.° 2 como número dentro de la cantidad, ocupando la sexta columna, él tendrá un valor de 200.000; en igual forma el N.° 4, como número que ocupa la quinta columna, valdrá 40.000; el mismo 4, como número que ocupa la primera columna, valdrá como 4 unidades. A este valor que tiene cada número según su posición en una cantidad, se le da el nombre de “valor relativo” de un número.